Krasorion.ru
Упаковочные материалы
Категории
Многочлен тейлора лотнера, многочлен тейлора и формула тейлора, многочлен тейлора для функции
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Содержание |
Определение
Пусть функция бесконечно дифференцируема в некоторой окрестности точки . Формальный ряд
называется рядом Тейлора функции в точке .
Связанные определения
- В случае, если , этот ряд также называется рядом Макло́рена.
Свойства
- Если есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
- Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Например, Коши предложил такой пример:
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
тогда: точка при или при : |
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- Пусть функция имеет производную в некоторой окрестности точки
- И производную в самой точке , тогда:
- — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)
Ряды Маклорена некоторых функций
- Экспонента:
- Натуральный логарифм: для всех
- Биномиальное разложение: для всех и всех комплексных где
- Квадратный корень: для всех
- для всех
- Конечный геометрический ряд: для всех
- Тригонометрические функции:
- Синус:
- Косинус:
- Тангенс: для всех где — Числа Бернулли
- Секанс: для всех где — Числа Бернулли
- Арксинус: для всех
- Арктангенс: для всех
- Гиперболические функции:
- для всех
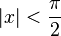
- для всех
- для всех
- для всех
Формула Тейлора для функции двух переменных
Пусть функция имеет полные производные вплоть до -го порядка включительно в некоторой окрестности точки . Введём дифференциальный оператор
- .
Тогда разложением в ряд Тейлора функции по степеням и в окрестности точки будет
где — остаточный член в форме Лагранжа:
В случае функции одной переменной , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе .
См. также
Литература
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10-24.
- Письменный Д. Т. Конспект лекций по высшей математике, изд.: АЙРИС-пресс, 2002.
Многочлен тейлора лотнера, многочлен тейлора и формула тейлора, многочлен тейлора для функции.
Файл:Portada Original de la Constitucion Mexicana de 1917.png, Категория:Списки проекта Музыка средней важности, Ferrari 275.